数学，
你这个磨人的小妖精！
上次超模君介绍了世界7大数学难题（传送门），很多模友表示连题目都看不懂。
所以，超模君今天就搜集了一些简单有趣的数学问题。
天使问题是由英国数学家约翰·何顿·康威（John Horton Conway）提出的一个博弈论问题，他在1982年出版的《Winning Ways》中描述了天使问题（the angel and the square-eater），现在通常被认为是天使和魔鬼的游戏。
假设有一个无限大的方格棋盘，天使和恶魔就在上面玩游戏。
在游戏开始之前，天使停留在棋盘上的某一点（天使的起点），获得指定权力 K （正整数），即每一轮天使可移动的方格数。
在每一轮游戏中，恶魔都在棋盘上放置一个路障，当然，路障不可以放在天使的停留处。
有恶魔开始放置第一个路障，然后天使就沿着棋盘上的方格移动K格（纵、横、斜的相邻方格均可），移动过程可以穿过路障，但是停留处不可是路障处。
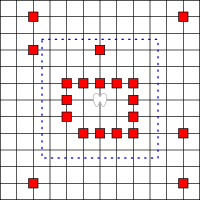
天使再次停留后，恶魔就设置第二个路障。。。
如此进行下去，如果在某一轮，天使停留在恶魔设置的某一个路障所在的方格中，恶魔就获胜；如果天使能无限地继续游戏，则天使获胜。
给出游戏规则后，康威提出了天使问题：一个能够获得足够权力的天使能赢吗？
为了激励有人来解决这个问题，康威提供了这样一个奖励方案：
①对于一个足够高权力的天使的获胜策略，奖励100美元；
②不论天使的权力如何，证明恶魔获胜的策略奖励1000美元。
而就在1982年，这个游戏设计者康威本人就证明了在以下两种情况下，恶魔有获胜的策略：
①当天使可移动的方格数 K = 1 时，恶魔有必胜策略；
②如果天使永远不会降低其 Y 坐标，则恶魔有必胜策略。
到了1996年，康威又证明了：如果天使一直增加它到起始点的距离，则恶魔有必胜策略。
康威心心念念的天使获胜策略还是没有人能提出来。。。
直到2006年，有四位数学家几乎是同时独立发现了天使的必胜策略：
布莱恩·鲍德奇（Brian Bowditch）证明了当K=4时，天使有获胜策略；
奥迪瓦·克洛斯特（Oddvar Kloster）和安德拉斯·马修（AndrásMáthé）证明了当K=2时，天使有获胜策略；
彼特·伽克斯（PéterGács）的证明仅适用于更大的常数。
不过，超模君还无法得知康威将奖励给了谁。
Thrackle问题也是康威提出来的，被称为“康威的恐怖问题”。
在一个图中，只有一些点以及点与点之间的连线，如果每一根线条都与其他所有线条刚好只相交一次，这个图就被称为是“thrackle”。
下图就是满足要求的3个thrackle：
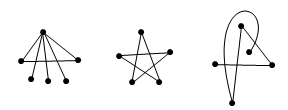
可以看出它们的一个特点：线条数都没超过顶点数。
而康威的Thrackle问题就是：是否存在线条数大于顶点数的thrackle？
有趣的是，像上面介绍的天使问题一样，康威也悬赏了1000美元来征解。（动不动就悬赏
）
只不过，到目前为止，还没有人能找得到线条数大于顶点数的thrackle，而目前已知的最好的结果是，一个 thrackle 的线条数不会超过顶点数的167/117。
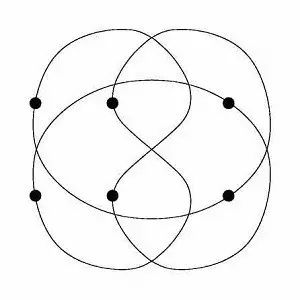
下图就是线条数和顶点数相同的一个thrackle（6个点、6条线），而此时想要在两个点之间添加一条线，使得这条线与其他所有线只相交一次，是不可能的！（各位模友可以尝试一下）
1958年的一天，美国数学家吉尔布雷斯（Norman L. Gilbreath）闲来无事，在餐巾纸上将一堆素数从小到大排成一行，然后又很无聊地将素数两两相减（相邻的两个素数，大的减去小的），得到第二行数，继续很无聊地减下去。。。
然后，见证奇迹的时刻到了！
吉尔布雷斯发现了一个规律：似乎从第二行开始，以后各行总是以1开头！
由此，吉尔布雷斯猜测：不论这个过程进行多久，上述结论总是正确的。并在1958年的一个数学交流会上提出了这个猜想，即吉尔布雷斯猜想。
第二年，吉尔布雷斯的两个学生凯尔格洛夫（R．B．Killgrove）和拉尔斯顿（K．E．Ralston）通过验证第63419个素数之前的所有素数而支持了这个猜想。
1993 年，数学家安德鲁·奥利兹科（Andrew Odlyzko）对 10 000 000 000 000 以内的质数（ 346 065 536 839 行）进行了检验，规律仍然遵循吉尔布雷斯猜想。
到目前为止，人们还没发现可以推翻吉尔布雷斯猜想的反例。
在了解利克瑞尔数之前，我们先讲讲回文以及回文数。（palindrome number）
“回文”（palindrome）是古今中外都有的一种常见的修辞手法和文字游戏，是指“顺着读和反过来读都能读通的句子”，古人喜欢用这种方式来体现两种食物之间的联系，甚至是得到相矛盾的结果。
例子：
①人人为我，我为人人。
②《易经．系辞》：日往则月来，月往则日来。
③英语中最著名的一个回文，是拿破仑被流放到Elba岛时说的一句话：Able was I ere I saw Elba.(在我看到Elba岛之前，我曾所向无敌。)
而在数学中，也存在具有这一特征的数字，即“正读反读都一样”的自然数，称为“回文数”，0是最小的回文数。
关于回文数的获取，有这样一个算法：
第一步：随机找一个十进制的数（如46），把它倒过来变成另一个数（64），再把这两个数相加（46+64=110），得到一个和数（110）；
第二步：将这个和数倒过来（011），再与原来的和数相加（011+110=121），又得到一个新的和数；
按照这个步骤，一步步往下算，直到得到一个回文数为止。（例子中的121已经是一个回文数，如果接着算下去，还会得到更多的回文数。）
既然方法如此简单而且有趣，人们纷纷加入这个回文数的探索之旅。
不过，人们慢慢发现，并不是所有数都像上面所举的例子那样只需要2步或者几步就可以得到一个回文数，数字89的“回文数之路”就非常漫长，足足要经过24步才得到第一个回文数：8813200023188。
随着计算机的发展，人们已经开始通过编写程序来获得回文数。
然而，有这样一个神奇的数字：196，专家表示打死都得不到回文数，因为他们按照上面的步骤用计算机进行了数亿次的迭代，还是无法得到一个回文数，像这种数，就称为“利克瑞尔数”（Lychrel Number）。
而现在的推论，196只认为是第一个可能的利克瑞尔数，因为还没得到任何有力的证明。
超模君表示不会轻易。。。
马上动笔算了起来！
196+691=887
887+788=1675
1675+5761=7436
7436+6347=13783
。。。
本文由超级数学建模编辑整理
部分资料来源于网络
转载请在公众号中，回复“转载”
↓↓↓《Python与机器学习》直通车
