编者按：
前面我们给大家推荐了江苏省初中数学文化节试题集《不一样的数学题——初中数学文化节试题精编与品评》，大家纷纷叫好。
☛
数学文化怎么考？
江苏省初中数学文化节14年的经验和积累告诉你
除了怎么考？
可能很多老师还关心数学文化节试题怎么用？
今天我们再分享中国数学奥林匹克高级教练满涛的经验，希望对大家有所帮助。
原文见该书的附录。
作者 | 满涛（中国数学奥林匹克高级教练）
好玩的数学（微信号：mathfun）编辑整理
2005年，大雪的时候，我还在南京大学工管院读书，那时还不是数学奥林匹克的教练员。有些中学生要参加第二十届江苏省初中数学竞赛，我给他们做辅导。后来，他们参加比赛了，赛后得到的初一组的试卷，让我吓了一跳。考查初中数学竞赛知识，还要写一篇名为《数轴的自述》的小作文?找到试卷一看，更是震惊，这不是一篇数学小作文的问题了…
整套试卷分为五个部分，每道试题均有恰到好处的小标题，有的是给予解题的提示，有的是试题背后的意义，考查的内容也均为七年级学习的东西，或者是很重要的数学内容，是谁有这么大本事命出了这么漂亮的试题？
2006年夏天，在扬中市参加江苏省数学学会夏令营，那时我28岁，是最年轻的教练员。第二次来夏令营，见过陈老先生、冯老先生、赵老先生、葛军大师、黄老师等前辈。我喜欢收集各位老师的讲义，作为自己今后教学的材料，所以下课后会游荡在各个教室，和学生们关系也很好。突然，发现了一份叫《奥数精神》的讲义，哎！不错哟。这位老师和其他教练都不ー样，讲义分为四个部分，智慧的光环、方法的力量、美的召唤、应用的广泛。我在本尊不知道的情况下，利用我不上课的间隙，偷偷地在最后一排听了他一节课。他的名字和讲义一样“霸气侧漏”，沙国祥老师——《奥数精神》，他对数学的理解让我惊叹，从简单问题着手，到复杂问题的本质，讲得很清楚；许多数学问题的本质是我第一次领略。
数学竞赛的问题多姿多彩，具有较强的挑战性。“无限风光在险峰”，在克服困难、迎接挑战的过程中，我们可以更深刻地感悟数学的本性及其文化内涵，领路数学文化的魅力，享受数学学习的乐趣。给我印象最深刻的是他的总结，三小时的课程，瞬间秒杀，我和同学们感受到了数学文化的乐趣。
课后，我和当时的数学会秘书长王肇西老师说，这位老师的奥数课程，让我体会很深，王老师也很高兴，他说这是初中数学竞赛的负责老师，那你把2003年到现在的我们夏令营的讲稿整理下。我花了一个多月通过自己整理和南大图灵文化的同志帮忙，整理好了讲义。最令我感兴趣的是沙老师历年的讲义，2003年《初中奥数中的数学思想方法》、2004年《品味奥数》、2005年《数学文化》以及2006年的《奥数精神》。我猜他肯定是数学文化节的“鼻祖”。
我从2006年开始，每年的第一个任务是自己打印《时代学习报》数学文化节的试题，作为我上课讲义的资料。十多年来，我上的提优和竞赛的课程大多数都是采用《时代学习报》数学文化节的试题作为例题
(当然未支付版权费)
。我觉得一周给孩子们上一节课，首先应该和学校课程紧密结合，第二应该给孩子们学习些有用的，未见过的，但促进孩子们课内学习的题目。
学习正负数时，我采用：
灵机一动
在学习加法交换律时，小华用小棒摆了一个等式(如图)。
突然有人问：“移动一根小棒，仍能是等式吗?＂小明、小丽眼疾手快，几平同时分别给出“8+6＝5+9”和“9+5＝6+8”。小华却另辟蹊径：
（请填写一个等式）
学生们很喜欢9变成一9，或者6变成一6后的等式。
在学习代数式时，我采用：
出手不凡
小亮刚学会“5以内的乘法口诀”，对于“5以上的两个一位数相乘”，小明用手势教小亮：如6×8，就用左手伸出1个手指，右手伸出3个手指(如图)，那么两手伸出的手指相加，得4，两手弯曲的手指数相乘，得8，于是可得6×8等于48。
按照上述方法：
(1)计算7×9时，左、右手伸出的手指数分别是多少？
(2)计算6×6时，结果是怎样得出来的？
(3)如果用 5+a 和 5+b 分别表示两个大于5的一位数，请说明上述“手算方法”的道理。
既学习了小九九的知识，也让学生自己列代数式，体会代数式能够证明结论的力量。
字斟句酌
甲乙两数比较大小，甲说：我的相反数比乙的相反数大。乙说：我的绝对值比甲的绝对值大。
(1)若甲乙两数异号，则甲乙的大小关系是
___;
(2)若甲乙两数同号，则甲乙的大小关系是___;
(3)分别在(1)、(2)两种条件下，比较甲乙及其相反数的大小关系。
万事皆备，只欠东风
已知两数a，b中，a＜b。
(1)只要再增加条件“______”，就一定能得到结论|a|＞|b|；
(2)只要再增加条件“______”，就一定能得到结论
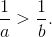
一道容易，一道较难，可以画数轴分类讨论得到结果，也可以用代数的方法证明，学生们很喜欢这样的题目。
有时学生们会跟着一起做游戏：
一一对应
有四项工作 x，y，z，w 随意地分配给四位工作人员a，b，c，d，每人做一项。图形是一种数学语言，“爬梯子”分配法用图形直观地表示工作安排：上边和下边分别写下参与的人员和工作项目，画好竖线和横线（如图(1)），然后“沿竖线从上向下行进，如遇橫线，即沿横线移到旁边的竖线上继续向下行进”，如此所得的工作分配结果如表1。
请在图(2)和(3)中添上横线，使之分别满足表2和表3所指定的工作分配。
同学们给出不同的解法，洋洋得意。
同学们有时也会得到自己的收获，比如：
一分为二
任何一个单位分数
都可以写成两个单位分数的和：
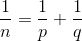(n，p，q都是正整数)。显然，这里的p，q都大于n。
如果设p＝n+a，q＝n+b，那么有
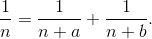
(1) 探索上式中的正整数a，b与正整数n之间存在什么样的关系(写出推理过程)；
(2) 写出
等于两个单位分数之和的所有可能情况。
通过(1)的代数证明，知道了小学在做形如(2)的问题时方法的笨拙，如果早知道这类问题的本质，也不至于小学阶段学得那么苦、那么乏味、那么痛不欲生。
数学的显著特点是它的理性。数学具有可靠性和必然性，因为除了极少的原理或公理以外，数学的结论都需要经过严格的证明，其典范是欧几里得的《几何原本》。学习数学，可以使我们思考、讲话、做事更加有条有理、客观公正，可以引导我们独立思考，摆脱盲从，探求万事万物内在的本质、原理和普遍规律，敢于质疑和创新。
数学思考同样需要细心的观察、敏锐的直觉、自由的想象、大胆的猜想。我国著名学者胡适说过：“大胆猜想，小心求证。”
如何判别好的方法：简单、明断、自然，直达本质，具有一定普遍性。
数学美在简洁、有序、对称、奇异。
至于实际教学，需要回到现实，但我以为学习每个章节、每个专题、每道例题，需要将解题的每一计算或证明步骤都搞清楚了，并不意味着就真正理解了解题的方法，特别是，要学会从直观、意义和来龙去脉等方面理解数学方法。好的方法反映了问题的本质，显得自然朴素，正确的推理计算保证了数学机体的健康，但仅有健康是不够的。
我从2009年起，开始给华杯赛供题，那时没有太多的想法，每次发现自己供的试题被选上，很开心，和少年宫黄利民主任一起欣赏被选中的试题。2010年，我把一些帯有数学文化节味道的题目发给了当时主试委员会的老师，把他们吓了一跳，紧接着就打电话问我这是怎么了？后来，两位老先生不同意，说文字太长，学生来不及阅读啊，但我感受到了他们对这些试题的好奇。后来，周春荔老师提出出一本《每日一题》，让我主写，当时唐保玲主任要求从第一届到第十二届的华杯赛题目中找一些活泼、难度不大、新颖又有新意的题目出来，编写365题，我找了很久，我在想，数学文化节的那么多题目不正是唐主任的要求吗?
所以这个小册子，全部使用了时代学习报数学文化节的题目，发给周教授时我在忐忑，老爷子要骂我的，一道华杯赛题都没选?没想到老爷子很开心，只是把前言中试题的选择范围修改了。
