专栏名称: SegmentFault思否
SegmentFault （www.sf.gg）开发者社区，是中国年轻开发者喜爱的极客社区，我们为开发者提供最纯粹的技术交流和分享平台。
目录
相关文章推荐
程序员的那些事  ·  印度把 DeepSeek ... ·  2 天前  
程序员小灰  ·  清华大学《DeepSeek学习手册》（全5册） ·  2 天前  
OSC开源社区  ·  宇树王兴兴早年创业分享引围观 ·  3 天前  
OSC开源社区  ·  升级到Svelte ... ·  4 天前  
程序猿  ·  “我真的受够了Ubuntu！” ·  3 天前  
51好读  ›  专栏  ›  SegmentFault思否

JS 数据结构与算法——栈 & 队列

SegmentFault思否  · 公众号  · 程序员  · 2019-01-21 08:00

正文

写在前面

原计划是把《你不知道的Javascript》三部全部看完的，偶然间朋友推荐了数据结构与算法的一套入门视频，学之。发现数据结构并没有想象中那么遥不可及，反而发觉挺有意思的。手头上恰好有《学习Javascript数据结构与算法》的书籍，便转而先把数据结构与算法学习。

一、认识数据结构

什么是数据结构？下面是维基百科的解释：

数据结构是计算机存储、组织数据的方式。 数据结构意味着接口或封装： 一个数据结构可被视为两个函数之间的接口 ，或者是 由数据类型联合组成的存储内容的访问方法封装

我们每天的编码中都会用到数据结构，因为 数组是最简单的内存数据结构 ，下面是常见的数据结构：

  • 数组（Array）

  • 栈（Stack）

  • 队列（Queue）

  • 链表（Linked List）

  • 树（Tree）

  • 图（Graph）

  • 堆（Heap）

  • 散列表（Hash）

下面来学习学习栈和队列。

二、栈

2.1 栈数据结构

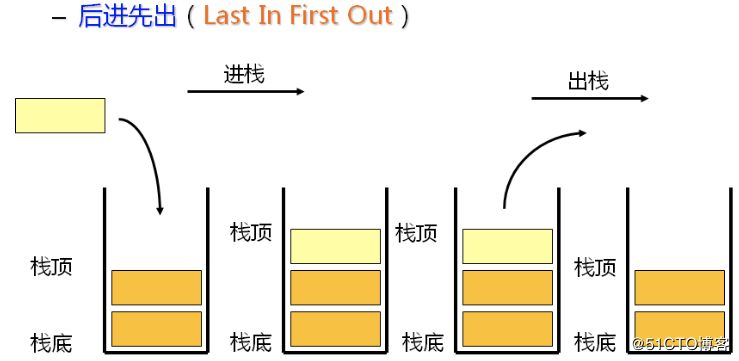
栈是一种遵循 后进先出（LIFO） 原则的有序集合。新添加的或待删除的元素都保存在栈的同一端，称作 栈顶 ，另一端就叫 栈底 。在栈里，新元素都接近栈顶，旧元素都接近栈底。

类比生活中的物件：一摞书📚或者推放在一起的盘子。

2.2 栈的实现

普通的栈常用的有以下几个方法：

  • push 添加一个（或几个）新元素到栈顶

  • pop 溢出栈顶元素，同时返回被移除的元素

  • peek 返回栈顶元素，不对栈做修改

  • isEmpty 栈内无元素返回 true ，否则返回 false

  • size 返回栈内元素个数

  • clear 清空栈 

  1. class Stack {
  2.   constructor() {
  3.     this._items 




    
= []; // 储存数据
  4.   }
  5.   // 向栈内压入一个元素
  6.   push(item) {
  7.     this._items.push(item);
  8.   }
  9.   // 把栈顶元素弹出
  10.   pop() {
  11.     return this._items.pop();
  12.   }
  13.   // 返回栈顶元素
  14.   peek() {
  15.     return this._items[this._items.length - 1];
  16.   }
  17.   




    
// 判断栈是否为空
  18.   isEmpty() {
  19.     return !this._items.length;
  20.   }
  21.   // 栈元素个数
  22.   size() {
  23.     return this._items.length;
  24.   }
  25.   // 清空栈
  26.   clear() {
  27.     this._items = [];
  28.   }
  29. }

现在再回头想想数据结构里面的栈是什么。

突然发现并没有那么神奇，仅仅只是对原有数据进行了一次封装而已。而封装的结果是： 并不去关心其内部的元素是什么，只是去操作栈顶元素 ，这样的话，在编码中会更可控一些。

2.3 栈的应用

（1）十进制转任意进制

要求： 给定一个函数，输入目标数值和进制基数，输出对应的进制数（最大为16进制）。 

  1. baseConverter(




    
10, 2) ==> 1010
  2. baseConverter(30, 16) ==> 1E

分析： 进制转换的本质——将目标值一次一次除以进制基数，得到的取整值为新目标值，记录下余数，直到目标值小于0，最后将余数逆序组合即可。利用栈，记录余数入栈，组合时出栈。 

  1. // 进制转换
  2. function baseConverter(delNumber, base) {
  3.   const stack = new Stack();
  4.   let rem = null;
  5.   let ret = [];
  6.   // 十六进制中需要依次对应A~F
  7.   const digits = '0123456789ABCDEF';

  9.   while (delNumber > 0) {
  10.     rem = Math.




    
floor(delNumber % base);
  11.     stack.push(rem);
  12.     delNumber = Math.floor(delNumber / base);
  13.   }

  15.   while (!stack.isEmpty()) {
  16.     ret.push(digits[stack.pop()]);
  17.   }

  19.   return ret.join('');
  20. }

  22. console.log(baseConverter(100345, 2)); //输出11000011111111001
  23. console.log(baseConverter(100345, 8




    
)); //输出303771
  24. console.log(baseConverter(100345, 16)); //输出187F9

（2）逆波兰表达式计算

要求： 逆波兰表达式，也叫后缀表达式，它将复杂表达式转换为可以依靠简单的操作得到计算结果的表达式，例如 ( a + b )*( c + d ) 转换为 a b + c d + * 

  1. ["4", "13", "5", "/", "+"] ==> (4 + (13 / 5)) = 6
  2. ["10", "6", "9", "3", "+",




    
 "-11", "*", "/", "*", "17", "+", "5", "+"]
  3. ==> ((10 * (6 / ((9 + 3) * -11))) + 17) + 5

分析： 以符号为触发节点，一旦遇到符号，就将符号前两个元素按照该符号运算，并将新的结果入栈，直到栈内仅一个元素 

  1. function isOperator(str) {
  2.   return ['+', '-', '*', '/'].includes(str);
  3. }
  4. // 逆波兰表达式计算
  5. function clacExp(exp




    
) {
  6.   const stack = new Stack();
  7.   for (let i = 0; i < exp.length; i++) {
  8.     const one = exp[i];
  9.     if (isOperator(one)) {
  10.       const operatNum1 = stack.pop();
  11.       const operatNum2 = stack.pop();
  12.       const expStr = `${operatNum2}${one}${operatNum1}`;
  13.       const res 




    
= eval(expStr);
  14.       stack.push(res);
  15.     } else {
  16.       stack.push(one);
  17.     }
  18.   }
  19.   return stack.peek();
  20. }
  21. console.log(clacExp(["4", "13", "5", "/", "+"])); // 6.6

（3）利用普通栈实现一个有 min 方法的栈

思路： 使用两个栈来存储数据，其中一个命名为 dataStack ，专门用来存储数据，另一个命名为 minStack ，专门用来存储栈里最小的数据。始终保持两个栈中的元素个数相同，压栈时判别压入的元素与 minStack 栈顶元素比较大小，如果比栈顶元素小，则直接入栈，否则复制栈顶元素入栈；弹出栈顶时，两者均弹出即可。这样 minStack 的栈顶元素始终为最小值。 

  1. class




    
 MinStack {
  2.   constructor() {
  3.     this._dataStack = new Stack();
  4.     this._minStack = new Stack();
  5.   }

  7.   push(item) {
  8.     this._dataStack.push(item);
  9.     // 为空或入栈元素小于栈顶元素，直接压入该元素
  10.     if (this._minStack.isEmpty() || this._minStack.peek() > item) {
  11.       this._minStack.push(item);




    

  12.     } else {
  13.       this._minStack.push(this._minStack.peek());
  14.     }
  15.   }

  17.   pop() {
  18.     this._dataStack.pop();
  19.     return this._minStack.pop();
  20.   }

  22.   min() {
  23.     return this._minStack.peek();
  24.   }
  25. }

  27. const minstack = new MinStack




    
();

  29. minstack.push(3);
  30. minstack.push(4);
  31. minstack.push(8);
  32. console.log(minstack.min()); // 3
  33. minstack.push(2);
  34. console.log(minstack.min()); // 2

三、队列

3.1 队列数据结构

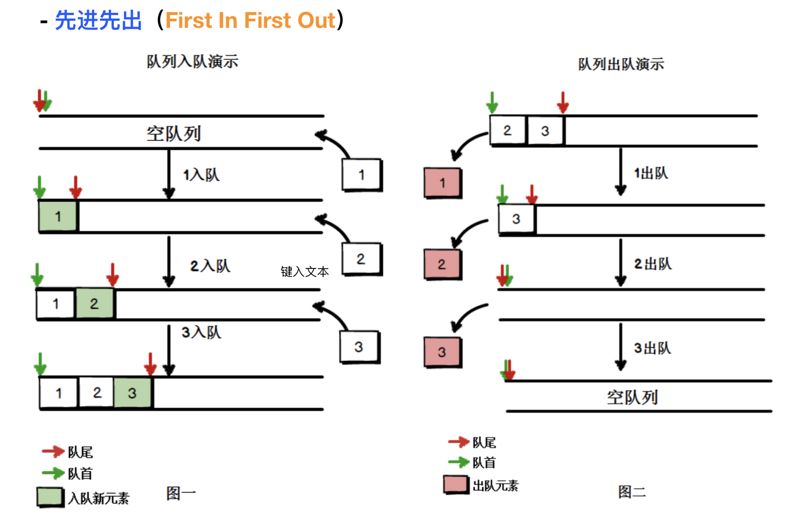
队列是遵循 先进先出（FIFO，也称为先来先服务）原则的一组有序的项。队列在尾部添加新元素，并从顶部移除元素 。最新添加的元素必须排在队列的末尾。

类比：日常生活中的购物排队。

3.2 队列的实现

普通的队列常用的有以下几个方法：

  • enqueue 向队列尾部添加一个(或多个)新的项

  • dequeue 移除队列的第一(即排在队列最前面的)项，并返回被移除的元素

  • head 返回队列第一个元素，队列不做任何变动

  • tail 返回队列最后一个元素，队列不做任何变动

  • isEmpty 队列内无元素返回 true ，否则返回 false

  • size 返回队列内元素个数

  • clear 清空队列 

  1. class Queue {
  2.   constructor() {
  3.     this._items = [];
  4.   }

  6.   enqueue(item) {
  7.     this._items.push(item);
  8.   }

  10.   dequeue() {
  11.     return this._items.shift();
  12.   }

  14.   head() {
  15.     




    
return this._items[0];
  16.   }

  18.   tail() {
  19.     return this._items[this._items.length - 1];
  20.   }

  22.   isEmpty() {
  23.     return !this._items.length;
  24.   }

  26.   size() {
  27.     return this._items.length;
  28.   }

  30.   clear() {
  31.     this.




    
_items = [];
  32.   }
  33. }

与栈类比，栈仅能操作其头部，队列则首尾均能操作，但仅能在头部出尾部进。当然，也印证了上面的话：栈和队列并不关心其内部元素细节，也无法直接操作非首尾元素。

3.3 队列的应用

（1）约瑟夫环（普通模式）

要求： 有一个数组 a [ 100 ] 存放0~99；要求每隔两个数删掉一个数，到末尾时循环至开头继续进行，求最后一个被删掉的数。

分析： 按数组创建队列，依次判断元素是否满足为指定位置的数，如果不是则 enqueue 到尾部，否则忽略，当仅有一个元素时便输出。 

  1. // 创建一个长度为100的数组
  2. const arr_100 = Array.from({ length: 100 }, (_, i) => i*i);

  4. function delRing(list) {
  5.   const queue = new Queue();
  6.   list.forEach(e => { queue.enqueue(e




    
); });

  8.   let index = 0;
  9.   while (queue.size() !== 1) {
  10.     const item = queue.dequeue();
  11.     index += 1;
  12.     if (index % 3 !== 0) {
  13.       queue.enqueue(item);
  14.     }
  15.   }

  17.   return queue.tail();
  18. }

  20. console.log(delRing(arr_100




    
)); // 8100 此时index=297

（2）菲波那切数列（普通模式）

要求： 使用队列计算斐波那契数列的第n项。

分析： 斐波那契数列的前两项固定为1，后面的项为前两项之和，依次向后，这便是斐波那契数列。 

  1. function fibonacci(n) {
  2.     const queue = new Queue();
  3.     queue.enqueue(1);
  4.     queue.enqueue(1);

  6.     let index = 0;
  7.     while(index < n - 2) {
  8.         index += 1;
  9.         // 出队列一个元素
  10.         const delItem = queue.dequeue();
  11.         // 获取头部值
  12.         const headItem = queue.head();
  13.         const nextItem = delItem






请到「今天看啥」查看全文


推荐文章
程序员的那些事  ·  印度把 DeepSeek 告上法庭！三哥的“既要又要”病又犯了？
2 天前
程序员小灰  ·  清华大学《DeepSeek学习手册》（全5册）
2 天前
OSC开源社区  ·  宇树王兴兴早年创业分享引围观
3 天前
OSC开源社区  ·  升级到Svelte 5后，我不会再用Svelte开发新项目
4 天前
程序猿  ·  “我真的受够了Ubuntu！”
3 天前
慈怀读书会  ·  听：遇见你是一种美丽的缘分
7 年前
时尚COSMO  ·  时髦办 | 连衣裙+乐福鞋，简单不粗暴的优雅
7 年前
中国航务周刊  ·  欧盟或于今日批准马士基收购汉堡南美
7 年前
赛柏蓝  ·  2017卖药再难也不怕！有这个帮你扛！
7 年前
上海发布  ·  【体育】客场带走一分，申花0:0战平广州富力！
7 年前
Sov5搜索   ·   小百科   ·   今天看啥   ·   移动版
51好读 - 好文章就要读起来!