编辑 | Gemini
例如:篮球比赛,还剩1点几秒时敌方进球,超我方2分。敌方在庆祝大局已定时,我方在1点几秒内一个超远三分出乎意料的绝杀!犹如奇迹的极限反杀的故事?
这是一场发生在十六世纪威尼斯的数学擂台赛。故事的主角是两个年轻的数学学者,Tartaglia和Fior。
Niccolò Tartaglia(1499~1557)是意大利著名数学家和工程师,16世纪著名的数学天才,被誉为弹道学之父。
Tartaglia小时候家里贫穷无法上学,他就用石子在石板上演算;经历了战乱让他的脸留下长长的刀疤并且伴有口吃。

就是这样一个艰难的人,不到三十岁就当上了威尼斯大学的数学教授。
在十五世纪以及更早的时候,人们早已掌握了一元二次方程的求根公式,但是西方数学界对于一元三次方程的求解迟迟没有进展。Tartaglia对于三次方程的求根有着浓厚的兴趣,他数学研究的主攻方向就是一元三次方程求根公式。
挑战他的另一位数学学者Antonio Fior (1506-?)的资质可就差远了,但他是著名数学家Scipione del Ferro(1465-1526)的关门弟子。Ferro 经过多年潜心研究,终于发现了一种缺项三次方程式(depressed cubic)的求根公式,即x^3+ax=b的公式,这无疑是一个重大突破。他把这一成果保密并在临终前传给了自己的关门弟子 Fior。
虽然 Fior 资质平平,但是他相信手握这一重大杀器依然能够横走于欧洲数学界。

这就是故事的背景。
1534年,Tartaglia宣布解出了一种缺项三次方程式的求根公式,与Ferro不同的是,他的公式是针对缺一次项的三次方程而言的,即x^3+ax^2=b。这一消息在欧洲数学界立马就炸开了锅。听到以后最着急的人当然是Fior,他想起了老师临终前传给他的杀器。毕竟是老师一生的心血,再不干点大事出来就要烂在手里了。
于是1535年,他向Tartaglia针对三次方程问题发起了挑战。数学擂台赛在16世纪的欧洲是很常见的场景,常见于数学家之间的学术斗争。此刻的 Tartaglia 正沉浸在丰收的喜悦里,自信心也有些爆棚,想也没想就答应了下来。双方各给对方出三十道难题,限定五十天内解出多者为胜。
这是 Fior 设的一个局,因为他知道 Tartaglia 是当时名望很大的数学家,只要能和大数学家打成平手,那么自己的名气和排位也将上升许多。用三次方程这一大杀器无疑是最好的选择。
Tartaglia 拿到题以后就后悔了,因为他发现这些题都是类似于x^3+ax=b这样的缺少二次项的形式,与他的成果对应不上。但是既然接受了挑战,他只能硬着头皮去解了。
Fior 拿到的这三十道题则是 Tartaglia 出的关于代数几何学方向的问题,资质平平的他当然无法解答。事实上他压根没有想着在五十天内解出来,只是希望 Tartaglia 在那三十道缺二次项的三次方程上面栽跟头然后跟他打个平手。
毕竟,Ferro 用毕生心血获得的成果是不可能在短短几十天内被 Tartaglia 攻破的。平局似乎已经显而易见了。而对于 Fior 来说,即便只是平局,仍然是一个伟大的胜利。
历史的经验告诉我们,弱者不要老想着通过搞个大新闻来扳倒强者。

比赛结束的前夕,Tartaglia 奇迹般地宣布解出了 Fior 的三十道题并公布了答案。最终擂台赛的比分是30:0。
Tartaglia 在短短几十天内冥思苦想独立解出了缺二次项的三次方程求根公式,这一极限反杀让 Fior 手里的“大杀器”终于烂在了手里。
随后的几年,Tartaglia 结合自己之前的成果苦心钻研,终于于1541年得到了一般形式三次方程(x^3+ax^2+bx=c)的求根公式。
但是同样地,Tartaglia 想把自己的求根公式藏起来闷声发大财。又过了几年,意大利人 Girolamo Cardano 经过软磨硬泡,加上自己的过人天赋终于从 Tartaglia 嘴里套到了公式。随后他的学生 Ludovico Ferrari 将其公之于众。使得 Tartaglia 在晚年无故地多了两个死敌。
当然这是另外一个故事了。
最后附上现在通用的三次方程求根公式。
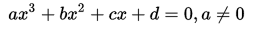
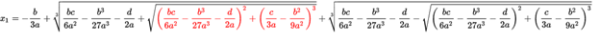
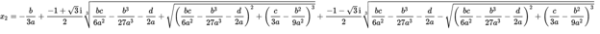
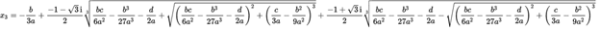

向先人致敬!

往期精彩文章:
-
第一个被认为“科学家”的人:泰勒斯
-
数学思维比数学运算更重要
-
二十世纪的十大科学骗局
-
瞎扯现代数学的基础
-
x背后的轶闻趣事
-
主宰这个世界的10大算法
-
16个让你烧脑让你晕的悖论
-
机器学习中距离和相似性度量方法
-
传说中的快排是怎样的
-
玻璃秘史:一个人 改变了全世界
-
程序人生的四个象限和两条主线
-
比特币的原理及运作机制
-
概率论公式,你值得拥有
-
分类算法之朴素贝叶斯算法
-
采样定理:有限个点构建出整个函数





