关于任意自然数倒数表为两个自然数倒数差的解集
作者:李骏
假设对任意自然数n,它可以表示为
1/n = 1/a
–1/b (1)
其中a,b为两个自然数,本文将讨论这个不定方程的解集并给出解数的一般计算公式.
引理1
设自然数n的互素的因子对的集合为M,而(1)式的解集为N;则N由M决定,或者说N与M之间是一一对应的,所以|N| = |M|.
证明:设a,b为 1/n = 1/a–1/b的一个自然数对解,a,b的最大公约数(a,b)= r,令
a =ra
1
b=rb
1
则 1/n = 1/[r(1/a
1
–1/b
1
)]
或 n = ra
1
b
1
/(b
1
-a
1
) (2)
因为b
1
-a
1
不能整除a
1
b
1
否则
因(a
1
,b
1
)=1,则有(b
1
-a
1
)| a
1
或
(b
1
-a
1
)| b
1
这都将与(a
1
,b
1
)=1矛盾.
所以 必有(b
1
-a
1
)|r
从而 (2)式可表为 n = ka
1
b
1
, k=r/(b
1
-a
1
)
因而 a
1
,b
1
是n的因子,且由(a
1
,b
1
)= 1可得出 a
1
,b
1
∈ M
就是说,N中的任意一个a,b 都可以找到一个对应的 a
1
,b
1
∈M
另一方面,对于任意的 a
1
,b
1
∈M,我们可以构造一个(1)的解。
a
1
,b
1
最小公倍数 [a
1
,b
1
] = a
1
b
1
/(a
1
,b
1
)=a
1
b
1
,而显然n是a
1
,b
1
的一个公倍数,所以有 a
1
b
1
|n
不妨假设b
1
> a
1
,令k=(b
1
-a
1
)n/(a
1
b
1
),a=ka
1
, b=kb
1
,则有
1/a-/1/b = (b
1
-a
1
)/(ka
1
b
1
)=1/n
这样 a,b∈N
综上,N与M之间可以建立一一对应关系,
所以|N| = |M|
证毕.
引理2
设自然数n的因子分解式为
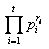 ,其中
为不同的素因子,
为对应指数,则n的互素因子对的集合M的元素个数|M|=
,其中
为不同的素因子,
为对应指数,则n的互素因子对的集合M的元素个数|M|=
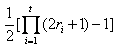 (3).
(3).
证明:我们对素因子个数t用数学归纳法.
t=1
,的时候n只有一个素因子,不妨设
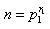 ,则显然n的素因子对只能是
,则显然n的素因子对只能是
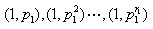 这
这
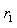 个
,
个
,
因此
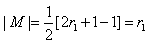 成立.
成立.
假设对t=m-1 (3)式成立.那么当t=m时,n 多了一个素因子
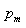 ,相应指数是
,相应指数是
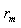 .
.
考虑n的全部素因子对集合M,可以分成三部分组成.
第一部分M
1
不含任何因子
,相当于t=m-1的情形,由假设|M
1
|=
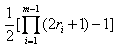
第二部分M
2
包含素因子
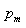 ,由于要求互素因子对,所以因子对中只可能有一个包含
,由于要求互素因子对,所以因子对中只可能有一个包含
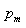 ,而
,而
M
2
={
任何第一部分M
1
中n的因子对中某一个因子乘上某个
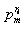
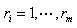 }
}
这样,一共有
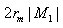 种组合.
种组合.
第三部分M
3
,仅由
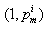
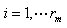 这样的因子对组成,一共有
这样的因子对组成,一共有
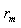 种组合.
种组合.
显然 M
1
,M
2
,M
3
两两相互的交集为空,
所以|M| = |M
1
|+|M
2
|+|M
3
|
=

=
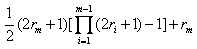
=
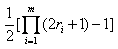
因此,对于t=m假设也成立.
综上,对于任意的因式分解,即对于任意自然数n,(3)都成立.
证毕.
定理1
设任意自然数n,(1)式的解集为N,则
|N| = 1/2(d(n
2
)-1)
,其中d()为
Dirichlet
除数函数.
证明:设
n
的因子分解式为
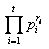 ,其中
,其中
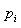 为不同的素因子,
为不同的素因子,
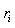 为对应指数,
为对应指数,
则
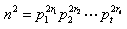
根据Dirichlet除数函数定义
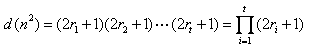
由引理1,2即可得证.
例子.
1.
n=60
因为 60 = 2
2
*3*5
所以解数为 1/2[(2*1+1)(2*1+1)(2*1+1)-1] = 22
2.
n=16
因为16 = 2
4
所以解数为 1/2[(2*4+1)-1] = 4
3.
n=7
解数为 1/2[(2*1+1)-1] = 1
4.
n=6000
6000 = 2
4
*3*5
3
所以解数为 1/2[(2*4+1)(2*1+1)(2*3+1)-1] = 94
注:关于(1)的解,实际上可以由引理1中的方法,由n的互素因子对全部构造出来。
《大历史》
与其说是一本书
倒不如说它是
一个全新的理念
是什么促使
比尔·盖茨
斥资千万
推行一项教育计划
?
是因为
大历史
打破了学科界限
摒弃针眼世界观
抵制知识碎片化的时代病症
综合
天文学、生物学、考古学、物理学、历史学
等多学科
为今天的读者提供统合性新知识
盖茨赞赏大历史
改变了
我们看世界的方式
它提供的新世界观
更新了
我们对历史和现实的认知
“大历史学派”开山之作
《时间地图:大历史,130亿年前至今》
Maps of Time: An Introduction to Big History

领先全网发售
出版社直接发货
包邮
先睹为快
长按二维码抢购







