AI科技评论按:本文由清华大学媒体与网络实验室以及迈阿密大学物理系共同合作完成,作者包括:余林韵(清华大学计算机系博士生,已毕业加入今日头条人工智能实验室)、崔鹏(清华大学计算机系副教授、博士生导师)、宋超明(迈阿密大学物理系助理教授)、张天扬(清华大学计算机系博士生)、杨士强(清华大学计算机系教授、博士生导师)。
在社交网络中,用户们会对周边用户的行为做出反应,这些在不同时间、空间发生的行为构成了社交网络中的信息流。其中,用户与用户间的交互行为是整个信息传播过程中最微观的指标,它对理解和揭示信息传播过程的形成和演化机制起到了基石性的作用,对其进行研究十分必要。

目前,学界中已尝试提出了一系列模型对用户行为动力学进行刻画。这当中,大部分模型假设了个体与个体之间的相互作用是高度随机的,遵循泊松过程。最近,一些工作在真实数据中发现,个体行为在响应时间维度(即一个人收到一个消息的时间到他做出一个响应的时间之间的持续时间)以及事件间时间维度(即同一人相邻两个行为之间的持续时间)均存在非常奇异的模式:
到底哪些才是用户行为动力学的基本要素?什么模型能够呈现出这些现象?目前,这些问题仍然没有一个明确的答案。
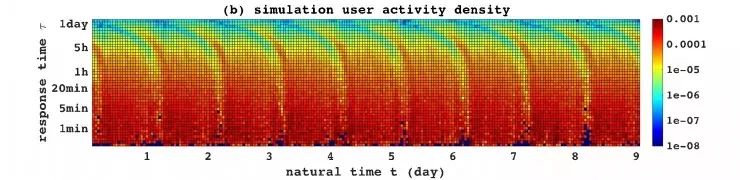
本文探索了一个由500万用户组成的大规模社交交互数据集,发现人类的交互行为动态呈现出极其复杂的特性。下图展示了用户交互行为在不同时间上的响应时间密度函数Pt(τ)。
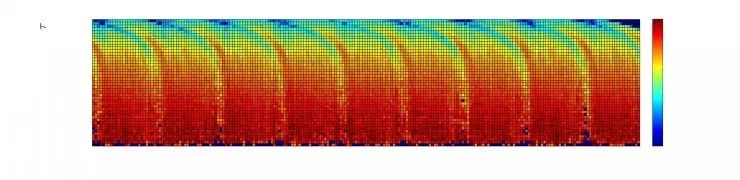
用户交互行为在不同时间上的响应时间密度函数Pt(τ),横坐标为t,纵坐标为τ
从图中可以很明显发现:随着响应时长的变化,用户的活跃度也不断发生变化。与此同时,响应时间密度函数在自然时间尺度也呈现出了周期性的变化趋势。这些现象表明,社会用户行为动力学在多重时间维度均存在异质性。尽管目前已有一些模型分别解决了用户交互行为在响应时间和人类行为昼夜变化的规律,但是这些模型均无法同时对这两个组成部分进行建模,导致在对用户交互行为进行建模和预测时产生偏差。
为考虑复杂的等待时间模式和人类不均匀的用户行为活动,作者根据自然时间变量 t 和响应时间变量 τ 设计了一个时序异质生存框架。它尝试回答如下问题:
如果在时刻发生了一个事件,经过一定时长之后出现对此事件的回应的概率是多少?如果经过了一定时长后仍然没有发生回应,此时它(响应)发生的概率是多少?
根据框架的目标,作者提出了三个度量指标:
1. 概率密度函数,记录事件从t 开始、响应持续时间为τ(在τ时间之后发生回复)的可能性。
2. 生存函数,累计函数的倒函数 1-CDFt(τ) ,给出了在 t+τ 之前没有发生响应事件的概率。
3. 危险函数,或称作强度函数,给出在t+τ时刻未发生响应事件的条件响应概率(t+τ时刻发生响应事件相对所有在t+τ前未发生响应事件的占比)。
给定这三个度量指标中的任意一个,另外两个指标也可被直接确定,其中危险函数通常具有最简洁的表达形式。因此,在生存模型比较复杂的情况下,一般会采用刻画危险函数的方式进行建模。

由于这是一个设计在概率框架下的模型,我们可以通过最大化对数似然的方式进行求解。利用微积分里的链式法则,我们只需要求出危险系数关于参数的偏导,就能方便的通过拟牛顿法得到参数的结果。
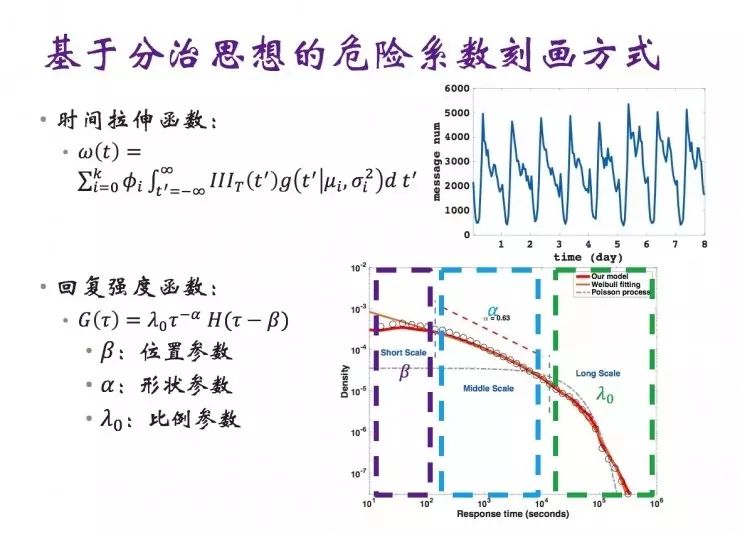
通常情况下,用户交互行为在自然时间和响应时间二个维度中的密度函数过于复杂,导致难以直接设计可被理解的危险函数。因此,我们利用了分治的思路以更好对危险函数进行建模:
首先,我们需要算法设计一个拉伸函数 ω(t),以表示用户在不同自然时刻的活跃度;
其次,算法还需要设计另一个响应函数 G(τ),用于刻画在不同响应时间τ上的回复强度的变化;
最后,我们通过下式将以上两个函数结合起来最终确定出危险函数的形式:
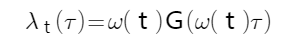
通过这种分解方法,本模型可以很容易构建出以前提出的所有模型。例如,当拉伸函数 ω(t) 在每个点保持相同的值(等于 1)时,危险函数将退化为: G(τ),等价于同质的生存模型;另一方面,当响应函数 G 保持不变时,危险函数将退化为:ω(t)乘以常数c,而此情况等价于异质泊松过程。
综上所述,同质生存模型和异质泊松过程所需要的所有特性都能通过这种分解模式在时序异质生存框架中得到体现。

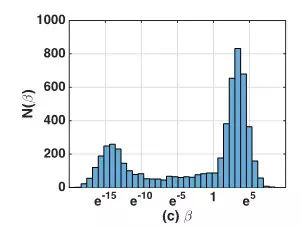
针对本文研究数据集的用户交互特性,我们设计了一个周期性的混合高斯模型来刻画时间的拉伸属性,之后,我们又设计了一个位移函数来刻画不同回复时长下的响应强度。其中,位置参数β主要控制用户的思考时间对短尺度回复时长响应强度的影响;形状参数α主要控制中尺度回复时长维度响应强度的幂律衰减斜率;而比例参数λ0主要描述长尺度回复时长维度的响应强度的指数衰减效应。
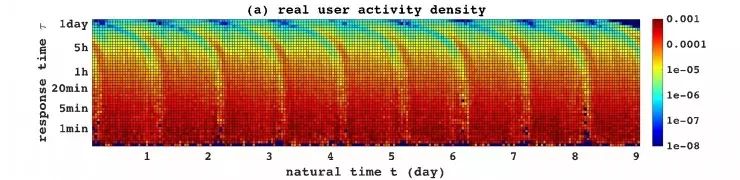
实验表明,我们的模型可以成功复现出社交交互数据集中用户的交互行为模式。从下文展示的对比图可发现,我们的模型模拟生成的结果的用户行为密度函数与真实情况是十分相似的。而在统计指标的对比中,本模型成功使得 77.1% 的数据同时通过了响应时长 KS-test 测试以及日常活跃度 KS-test 测试,准确率相较已有方法提升了 36.6%。

准确率提升:36.6%
此外,由于我们模型的参数具有明确的物理意义,我们对模型中用户响应函数的参数进行了进一步分析,试图挖掘出用户的行为倾向。
首先,参数β的分布形式是一个有两个峰的联合分布。其中,接近0点的峰值表明,一大批网络中的用户是乐于不经思考便无脑回复的。相比之下,另一部分用户通常会在回复前对信息进行更谨慎的判定和思考。对于后者,我们应该更加专注于所发消息的品质,以吸引这部分用户更好得帮助我们分享信息。
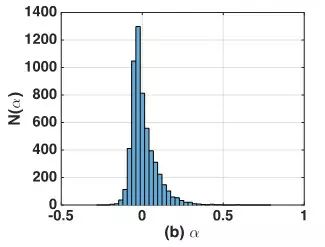
参数α描述了不同时长对用户回复的影响。其中,当α>0时,回复概率随时间流逝逐渐变低,是一个早衰过程;α=0时,回复概率与时间无关;α<0时,回复概率随时间流逝逐渐变高。
在我们的数据集中,参数α服从正态分布,其中有36.4%用户α>0.01,对于这部分用户,他们回复概率随时间流逝逐渐变低,因此,我们需要仔细考虑给这些用户发消息的时间,以提升这些用户回复消息的概率。
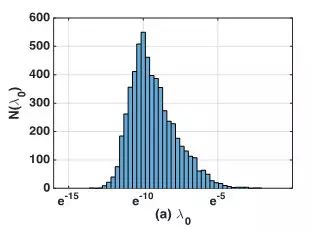
最后,比例参数λ0主要控制了响应时长的指数衰减,在我们的数据集中,λ0服从了e-10的LogNormal分布,其较小的值说明了网络中的用户对该网络有着较大的粘性。
总结:本文提出了一个综合性的时序异质用户动力学生存框架,框架能够同时对用户交互行为在响应时间维度和自然时间维度的影响进行刻画。通过为框架设计的一般性分解方案,该框架涵盖了目前针对用户交互动力学行为设计的所有模型。
由于该框架是在概率框架下进行设计的,模型可方便得通过最大似然法来进行求解。之后,本文对一个大规模的社交网络用户交互行为数据集进行了观察,并根据其中的用户行为特性进行了针对性的建模,模型中的参数具有明确的物理意义,其数据分布有助于对社会动态的基本规律进一步进行理解,并可针对性的为用户设计推广方案。实验证明,本模型可以成功复现出社交交互数据集中用户的交互行为模式。相比当前方法,模型在统计指标上获得了很大的提升。此外,模型在多个数据集上均展现出了很高的准确率,表明其具有很强的泛化能力。
————— 给爱学习的你的福利 —————
随着大众互联网理财观念的逐步普及,理财规模随之扩大,应运而生的智能投顾,成本低、风险分散、无情绪化,越来越多的中产阶层、大众富裕阶层已然在慢慢接受。王蓁博士将以真实项目带你走上智能投顾之路,详情请识别下图二维码或点击文末阅读原文~

————————————————————


















