作者 | 大小吴
来源 | 大小吴的数学课堂
2020 年先祝大家新年快乐！出门记得戴口罩哟~
呆在家大家可能都闷坏了吧，大小吴今天来给大家解解闷，我们来说说游戏的那些事。
俄罗斯方块大家都不陌生吧！为了怀旧，大小吴还特意买了游戏机充电宝。
大家在玩俄罗斯方块的时候有没有想过这样一个问题：如果玩家足够厉害，是不是永远也玩不死？换句话说，如果你是万恶的游戏机，你知道游戏任意时刻的状态，并可以有针对性地给出一些不合适的方块，尽量迫使对面的玩家面对最坏的情况。那么，你有没有一种算法能保证害死玩家呢？
1 俄罗斯方块中的循环
我们先来回忆一下俄罗斯方块的游戏界面：
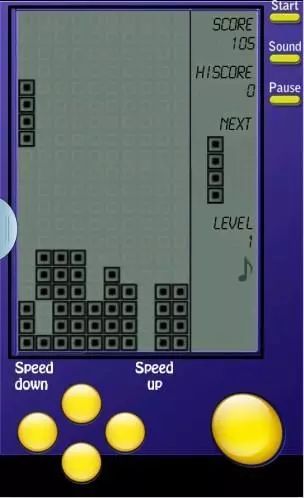
俄罗斯方块区域是一个宽为 10，高为 20 的矩形，并且玩家可以看到下一个方块是什么。
相信很多人都有过这样的经历：玩俄罗斯方块的时候，如果开局就给你一个 S 形方块，这会让完美主义者感到崩溃。
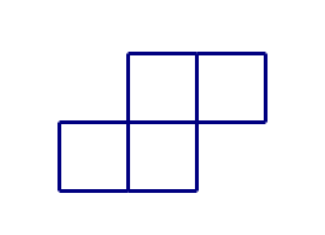
如果第二个还是 S，第三个仍然是 S，那我们可能就放弃重新开始下一局了。
那么，假如游戏机真的给你无穷个 S 形方块，玩家是不是没有解了呢？
答案是否定的！
我们看下图：
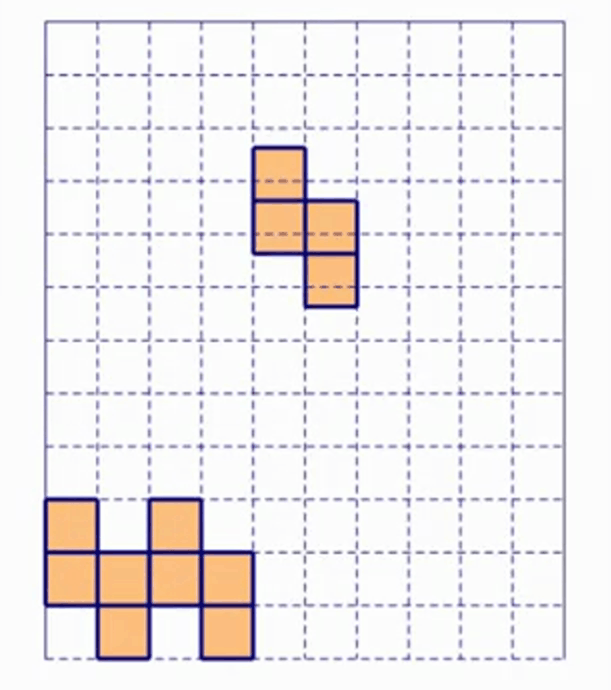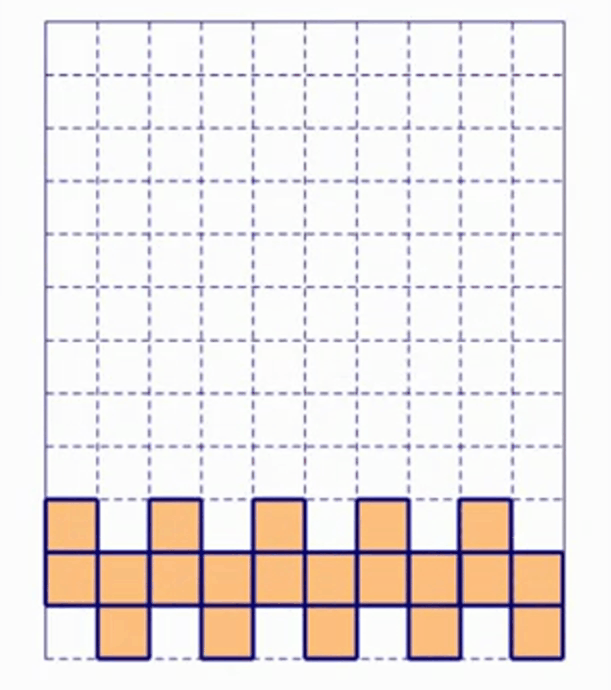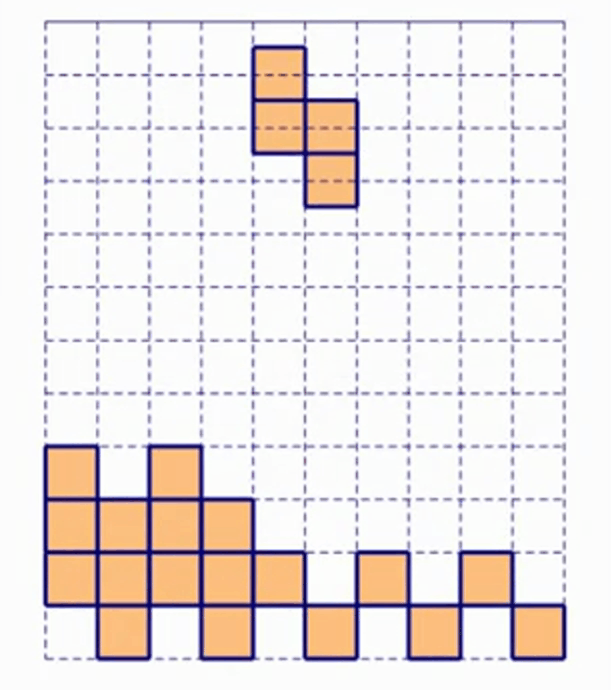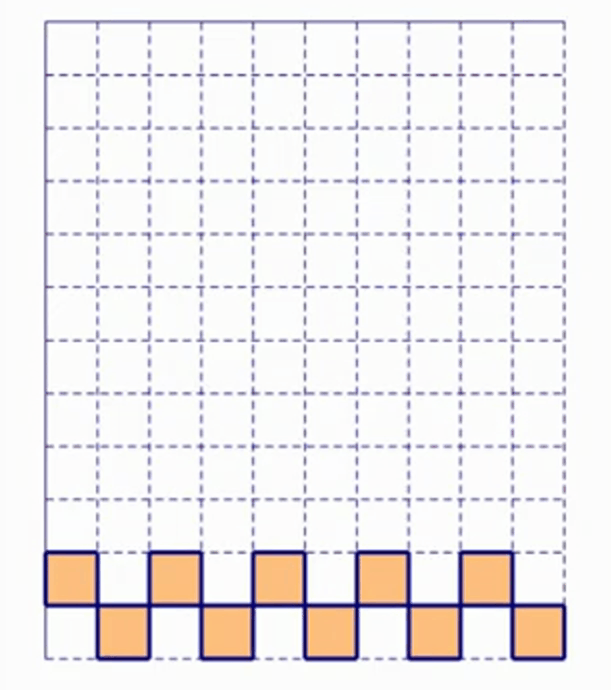
我们会发现，只要机器给的一直是 S 形方块，玩家可以不断重复这几个步骤，保证永远也不会死。
不过，这个循环是在游戏场地清空的情况才产生的。
要是玩着玩着，机器看着你局势不好时突然给你无穷多个 S 形方块呢？事实上，此时局面的循环依然存在。
在第 5 个 S 形方块落地后，循环再次产生。
2 俄罗斯方块中的“通道”
俄罗斯方块究竟是否存在必死的情况呢？
1988 年，约翰·布茹斯托斯基的一篇论文给出肯定的答案。他给出了一种算法，可以保证游戏机能够害死玩家，即使要求它必须提前向玩家展示下一个方块的形状。
我们将两次重复状态及其之间的游戏过程叫做一个“
循环
”，这个循环实际影响到的那些行叫做“
实际循环区
”。例如前文提到的一种情况就是一个循环，这个循环的“实际循环区”是从第 4 行到第 7 行。
我们把宽为 10 的游戏区域划分为
5 个宽为 2
的“
通道
”，从左至右用 1 到 5 标号。注意到前文中提到的两个循环都有一个共同点：每个 S 形方块最终都完全落在某个通道内。也就是，如果游戏机一直给你 S 形的方块，只要所有 S 形方块的下落位置
都没有跨越通道
（如下图中的 A、B 那样）
，你就能弄出一个循环！
为了证明上述这一点，我们对通道编号实施归纳。
考虑命题
：如果某个 S 形方块
（或它的一部分）
落在了通道
的左边
（或者说是前
列里）
，那它一定完全落在某个通道内。
：成立，方块不可能落到通道 1 左边的格子，因为通道 1 左边什么也没有。
假如
为真，下面我们说明
为真。
在说明
为真之前，我们首先来证明一个
引理
：在循环中的任意时刻，通道
的实际循环区内绝不可能出现形如“
”的两个并排的格子。
如下图所示:
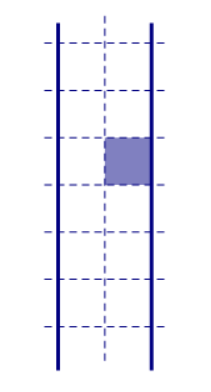假设图形阴影部分方块是在通道
的实际循环区内最低的
的结构。假如这一行被消掉，由归纳假设，不存在 S 形方块跨越该通道左边界，因此只有一种可能，某个 S 形方块从左侧挤了进来，如下图所示。但这样就产生了一个更低的
，矛盾。证毕。
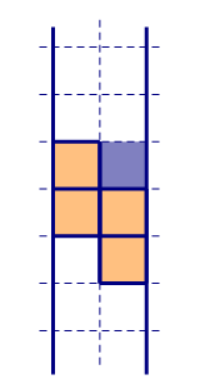接下来，我们来说明
为真。
要想让 S 形方块占据通道
