| SHAROON SAXENA
编译 | VK
来源 | Analytics Vidhya
概述
-
-
博弈论对人工智能来说是一个基本概念，我们觉得每个人都应该知道
-
在这里，我们通过举例深入研究博弈论，并将其与人工智能联系起来
介绍
我想先问一个简单的问题——你能认出下图中的两个人吗?
我肯定你说对了。
对于我们这些早期数学发烧友来说，电影《美丽心灵》(A Beautiful Mind)已经深深地印在了我们的记忆中。
Russell Crowe在电影中扮演John Nash，一位诺贝尔经济学奖得主(上图左侧)。
现在，你应该还记得那个经典场景:“不要追金发女郎”。
在这个场景中，约翰·纳什引用道:
“当团队中的每个人都在做对自己和团队最有利的事情时，最好的结果就会出现。”
许多人认为这是著名的“纳什均衡”的发现。
虽然这场景很经典，但也不一定是对的。
这个场景实际上描述了“帕累托最优”。
但这对我们理解博弈论还是有帮助的。
所以在这篇文章中，我们将鸟瞰博弈论。
我们还将讨论博弈论在人工智能领域的应用。
我以一种即使是初学者和非技术人员也能跟上的方式来写这篇文章。
目录
-
-
-
-
什么是博弈论?
什么是博弈论?我相信你在某个时候曾经遇到过这个概念，但从来没有真正深入研究过它。
相信我，在人工智能领域，这是一个耐人寻味的话题。
我们先来给博弈论下一个正式的定义。
博弈论可以被认为是两个或多个理性的代理人或玩家之间相互作用的模型。
在这里，我必须强调
理性
这个关键字，因为它是博弈论的基础。
但理性究竟意味着什么呢?
我们可以简单地把理性称为一种理解，即每个行为人都知道所有其他行为人都和他/她一样理性，拥有相同的理解和知识水平
。
同时，理性指的是，考虑到其他行为人的行为，行为人总是倾向于更高的报酬/回报。
简而言之，每个行为人都是自私的，都试图使报酬最大化。
既然我们已经知道了理性意味着什么，让我们来看看与博弈论相关的其他一些关键词:
-
游戏
:一般来说，游戏是由一组玩家，行动/策略和最终收益组成。
例如:拍卖、象棋、政治等。
-
-
-
-
-
收益
:收益是所有玩家在获得特定结果时所获得的奖励。
它可以是正的，也可以是负的。
正如我们之前所讨论的，每个代理都是自私的，并且想要最大化他们的收益:
博弈论中的纳什均衡
纳什均衡是人工智能博弈论方法的“基石”。
纳什均衡是每个玩家选择的行动满足:
“没有玩家会想要改变他们的行动。从纳什均衡中改变他们的行为意味着他们没有达到最佳状态"
或
“考虑到其他所有代理人都是理性的，他们都为他们自己选择最好的行动，纳什均衡产生的行动对我来说是最好的。”
任何玩家都不可能通过改变之前的决定来增加收益。
我们也可以将其视为“
无悔
”，即一旦做出决定，玩家便不会因为考虑到后果而后悔。
为了了解纳什均衡的作用，我们现在来解决博弈论中最常见的问题——
囚徒困境
。
这个游戏是一个经典的例子，它说明了在代理人只关心自身利益的情况下，为了共同利益而协同行动的困难。
在这个游戏中，我们有两个犯人，Alan和Ben，他们因为同样的罪行被抓了起来，被关在两个不同的审讯室里。
他们有两个选择:
-
保持沉默
-
承认罪行
假设每个人都有两个选择。
总共有4种结果:
-
{沉默,沉默}
-
{承认,沉默}
-
{沉默,承认}
-
{承认,承认}
这4个结果可以方便地表示为一个博弈矩阵:
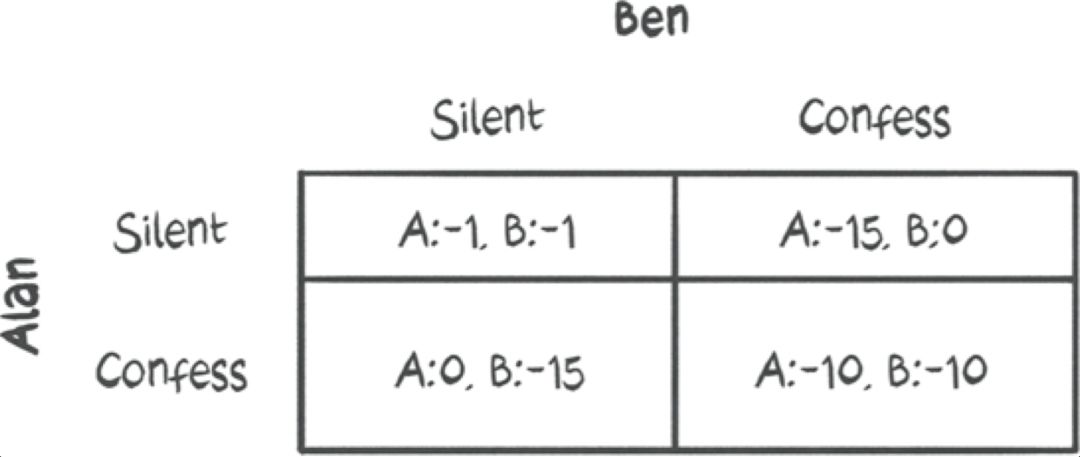在这个表达式中，支付的形式是(Alan的支付，Ben的支付)。
沿着行，我们有Alan的动作，沿着列，我们有Ben的动作。
好好思考收益。
为什么有收益是负的?这是因为，根据他们的行动，他们将获得预先确定的监禁年限。
-
-
如果他们中的任何一人认罪，认罪的人将获得自由，而另一名囚犯将被判15年监禁
-
这一困境的出现是因为两个囚犯都不知道另一个囚犯做了什么。
那么，你认为这个问题中的纳什均衡产生的结果是什么呢?人们凭直觉大概是认为犯人会互相合作，保持沉默。
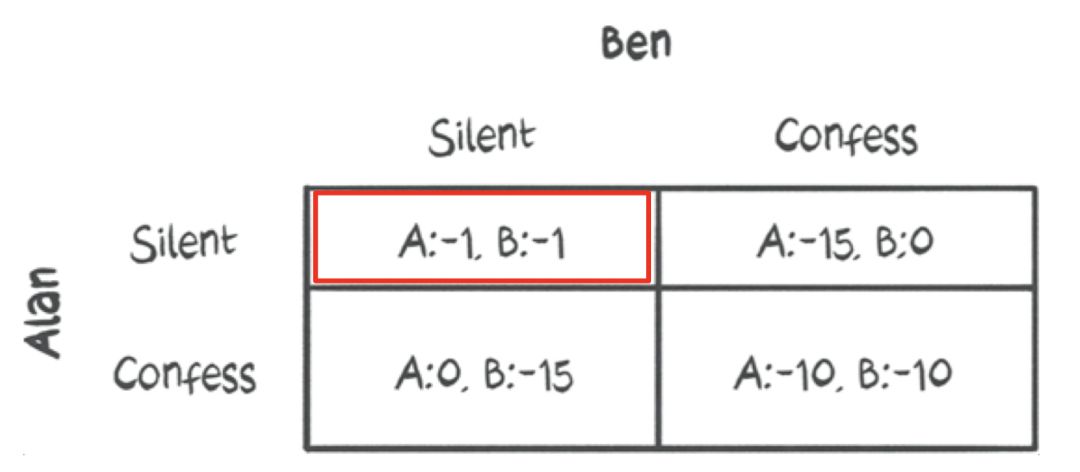但我们也知道，囚犯会尽力减少他们所受的监禁，这关乎他们的个人利益。
即使他们保持沉默，他们仍然会被监禁一年。
Ben也会这么想。
如果我们专注于博弈矩阵，思考过程将会变得非常有趣:
-
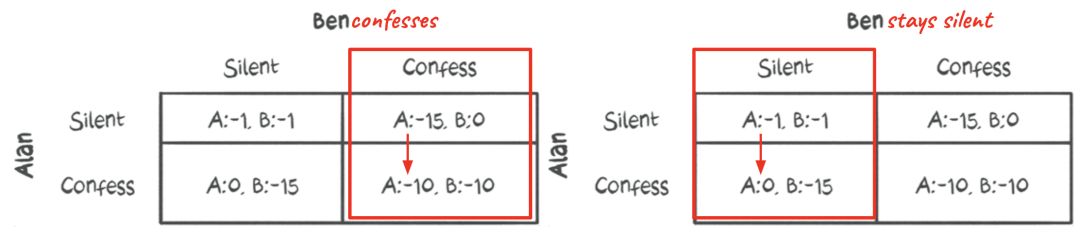
在Ben坦白的情况下，Alan最好的选择就是坦白。这将导致10年的监禁而不是15年
-
如果Ben保持沉默，Alan最好还是坦白，因为如果他也保持沉默，他将面临一年的监禁，而不是一个自由人
所以这个博弈矩阵和Alan的想法是完全一致的。
现在，如果Ben也有同样的想法，博弈矩阵对他来说应该是这样的:
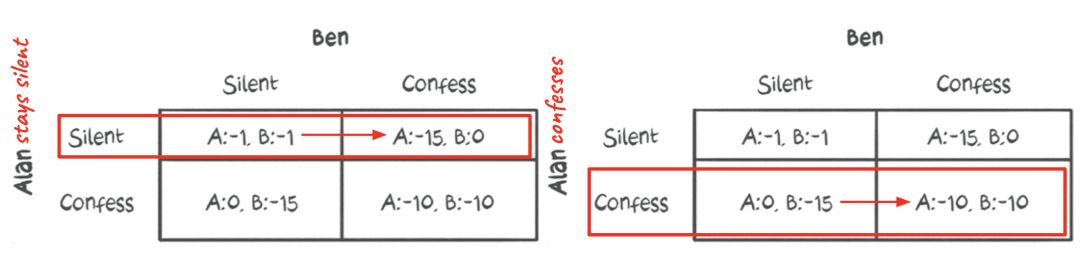假设Ben也像Alan一样经历了理性思考过程。
Ben还得出结论，无论艾伦选择什么，坦白总是有益的。
现在，如果我们把这两个囚犯的理性思维叠加起来，结果是这样的:
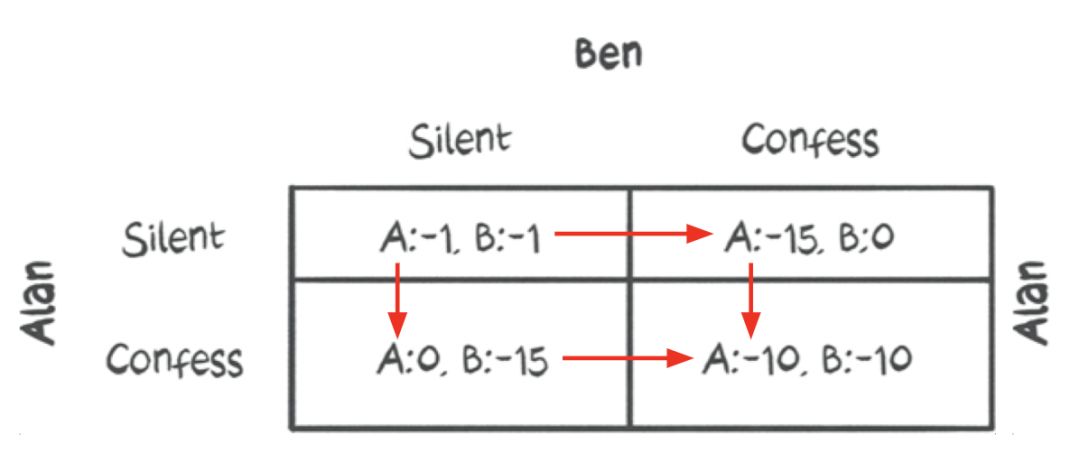从结果来看，最好的策略是{坦白，坦白}。
即使他们中的任何一个试图偏离这个动作，他们的情况也比他们通过玩这个动作所得到的更糟。
因此，{坦白，坦白}是一种纳什均衡策略
。
很有道理，对吧?对于纳什均衡，我们可以得出这样的结论:对于任何游戏来说，它都是一个“
无悔
”的解决方案，但不一定是最优的。
博弈类型
我们刚刚看到一个囚徒困境的例子，两个囚徒必须同时做出决定，我们用一个博弈矩阵来表示。
这些类型的博弈通常被称为正则形式的博弈
。
在博弈论中，游戏可以根据许多不同的标准分为许多不同的类别。
代理之间的交互
直观上，我们可以根据游戏中的代理是竞争还是合作来区分游戏。
政治竞选就是一个竞争游戏的好例子，一个候选人的奖励导致另一个候选人的失败。
另一方面，一场篮球比赛可以被看作是一场合作的比赛，每个球员如果互相合作就会得到更多的奖励。
代理怎么进行游戏
我们还可以根据游戏是否同时存在或是否具有广泛性来对它们进行分类
。
为了理解这一点，让我们以一个名为“性别之战”的问题为例。
考虑到Bob和Amy两个经常一起玩。
他们很清楚对方分别喜欢出去踢足球和参加舞会。
这次他们决定这次一起出去玩，他们可以给对方一个惊喜或者各自玩自己的。
如果他们打算给对方一个惊喜，他们并不知道对方的周末计划。
博弈矩阵描述了4种不同的情况:
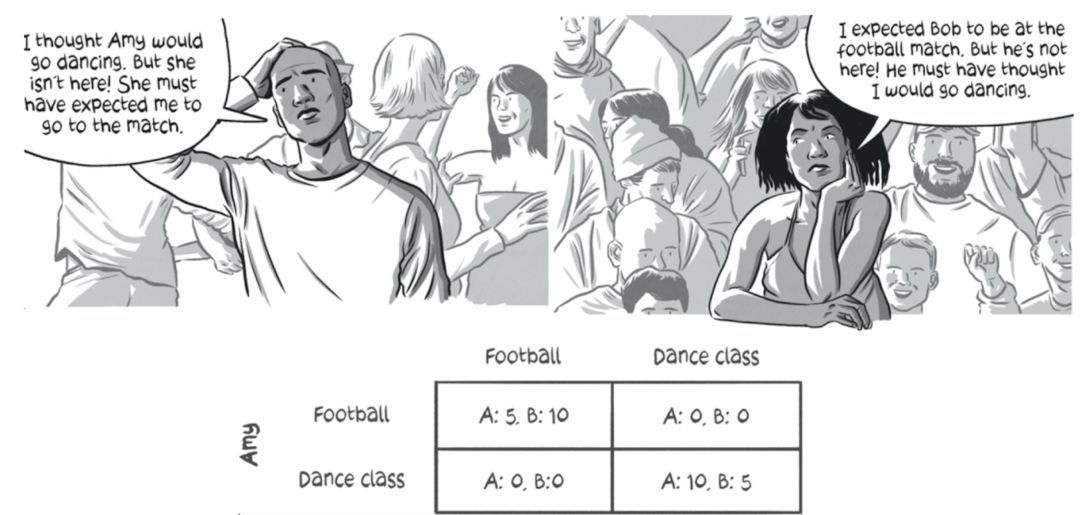
博弈矩阵清楚地解释了如果Bob和Amy彼此不配合，他们就得不到任何回报。这是一个同时进行的游戏的例子，在这个游戏中，两个玩家同时行动，并且事先不知道其他玩家的行动。
另一方面，如果他们通过告诉对方自己的行动来相互配合，游戏的形式如下:
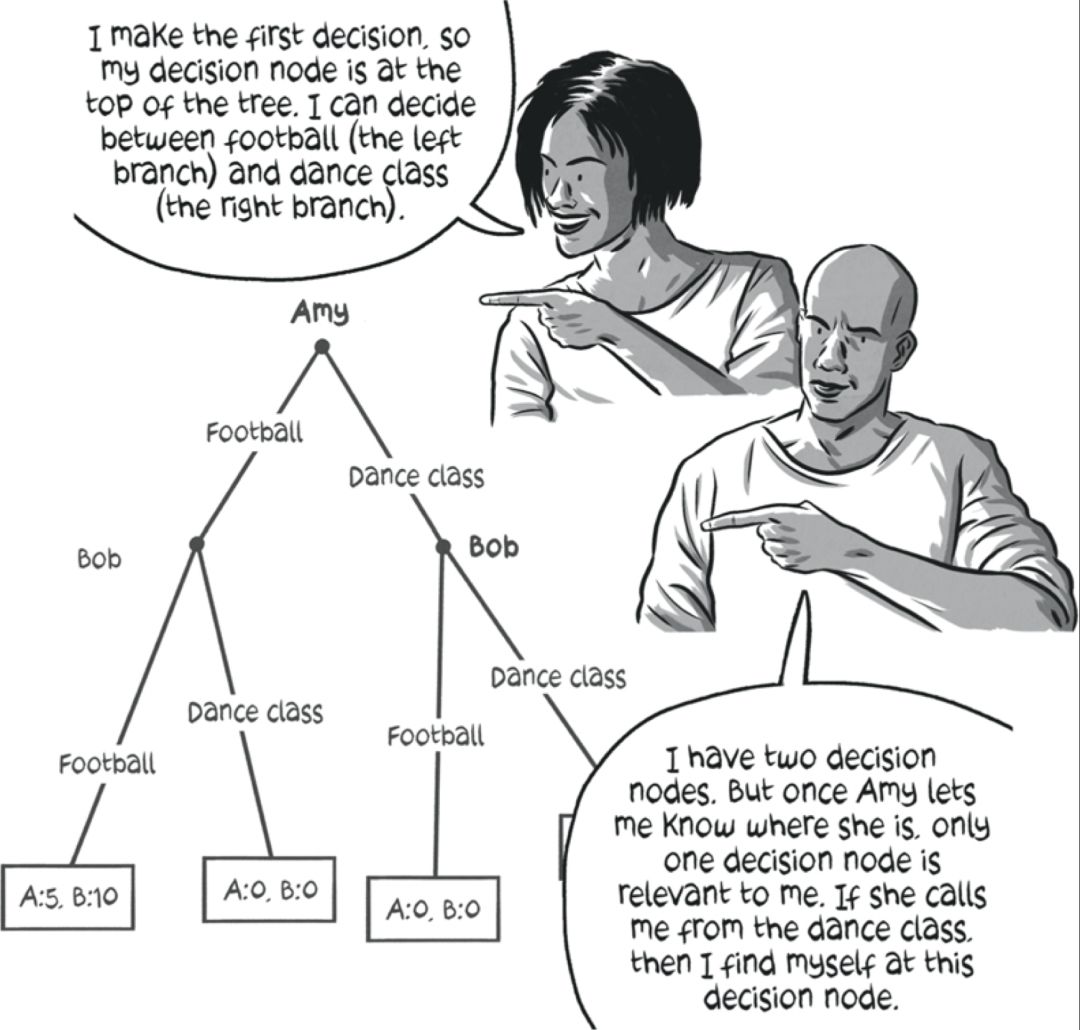
这是一个广泛的形式游戏或“回合制游戏”的例子。
在这里，每个玩家都可以看到其他玩家在玩什么动作。
这是另一个直观的例子——石头-剪刀-布的游戏是同时进行游戏中的一个很好的例子。
另一方面，井字棋游戏是一种广泛的形式游戏。
信息
在博弈论中，经常会出现这样的情况:玩家的信息不完整。
他们可能不知道其他玩家所有可用的策略或潜在的回报。
玩家可能不知道他们在和什么样的人打交道，也不知道他们的动机是什么。
根据玩家对其他代理的了解程度，游戏大致可以分为三类:
完美信息:
在完美信息中，每个代理都知道:
-
其他代理可能采取的所有操作
-
他们在做什么
-
他们得到了多少回报
井字游戏和国际象棋就是很好的例子。
在现实世界中，完美信息游戏非常罕见
。
此外，机器学习和深度学习方法在这些游戏中也非常有效。
不完美信息:
在这种情况下，行为人知道其他行为人的性质和动机，以及在所有可能的结果中他们会得到多少回报。
但他们不知道自己在做什么。
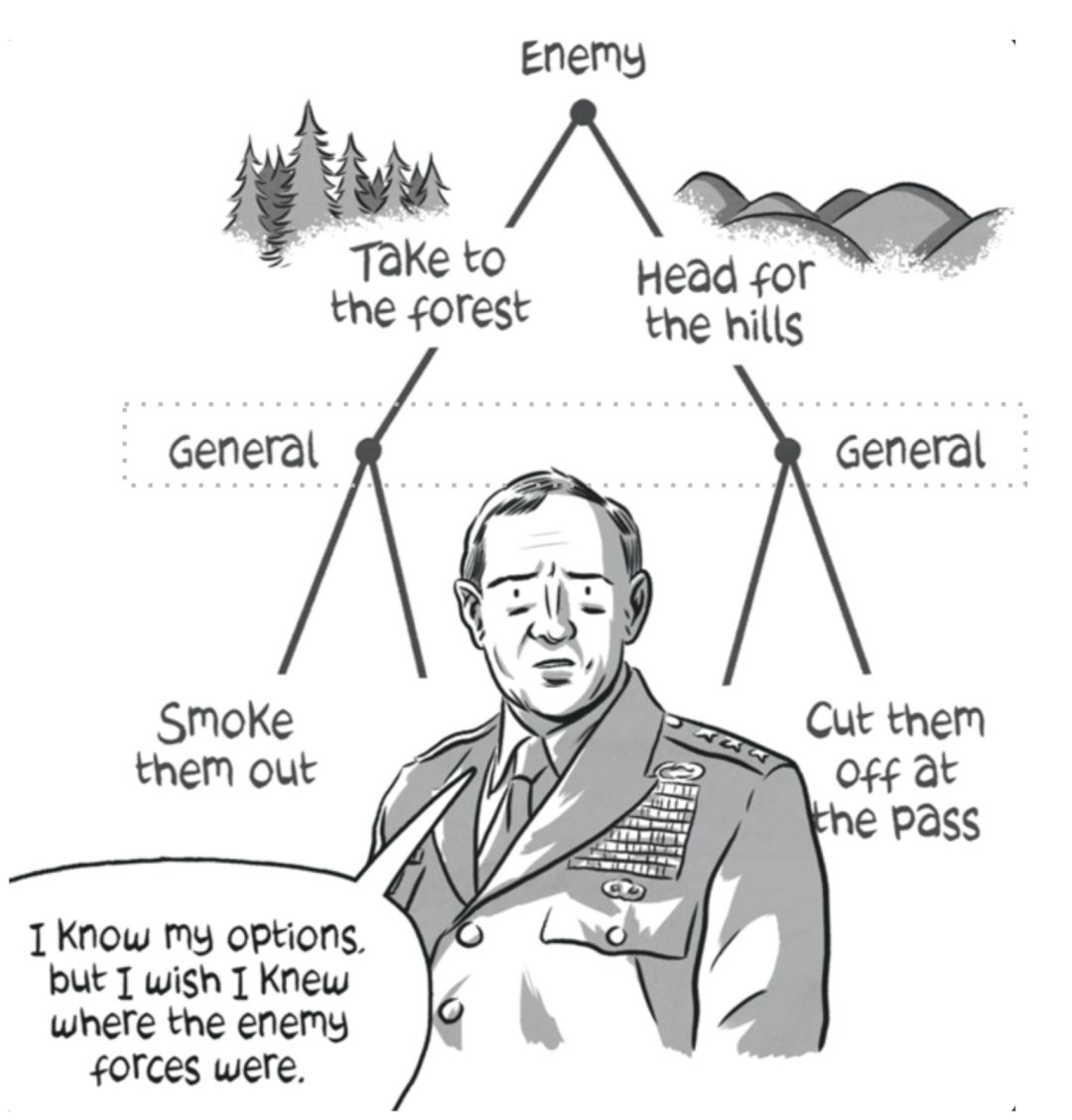
在这里，将军知道在每个可能的情况下敌人的动机和回报。
但他不知道敌人藏在哪里。
因此，将军不知道他所在的确切决策节点(用虚线框表示)。
不完全信息游戏在现实场景中经常遇到。
不完全信息
不完全信息是一种非常紧密地模拟现实世界的情况。
在这里，代理没有关于其他代理的“类型”的信息。
即使任何给定的代理能够看到其他代理所采取的操作，他/她也不知道其他代理的动机，也不知道其他代理将从该操作中获得什么奖励。
从本质上说，不完全信息博弈是最普遍的博弈形式。
扑克是一个典型的不完全信息游戏的例子，因为玩家不知道对手手里拿的是好牌还是坏牌。
我们对扑克游戏特别感兴趣，因为它的不完全信息的性质使它很好地代表了现实世界。
正因为如此，它一直被认为是不完全信息博弈的人工智能领域的一个基准问题。
人工智能中的博弈论
啊——你一定想知道这一切在人工智能的背景下意味着什么。
这些不同类型的游戏和信息与人工智能有什么关系?好吧，让我们来看看!
就人工智能而言，博弈论基本上有助于做出决策。
考虑到“理性”是博弈论的基础，这并不难。
事实上，博弈论已经开始在人工智能中确立自己的地位——你能猜到它在哪里吗?
其中一个是生成对抗网络(GANs)的概念。
它们被引述如下:
“这是过去二十年来机器学习中最酷的想法。”——Yann LeCun，人工智能和深度学习领域的领导者之一
那么博弈论是如何帮助GANs的呢?
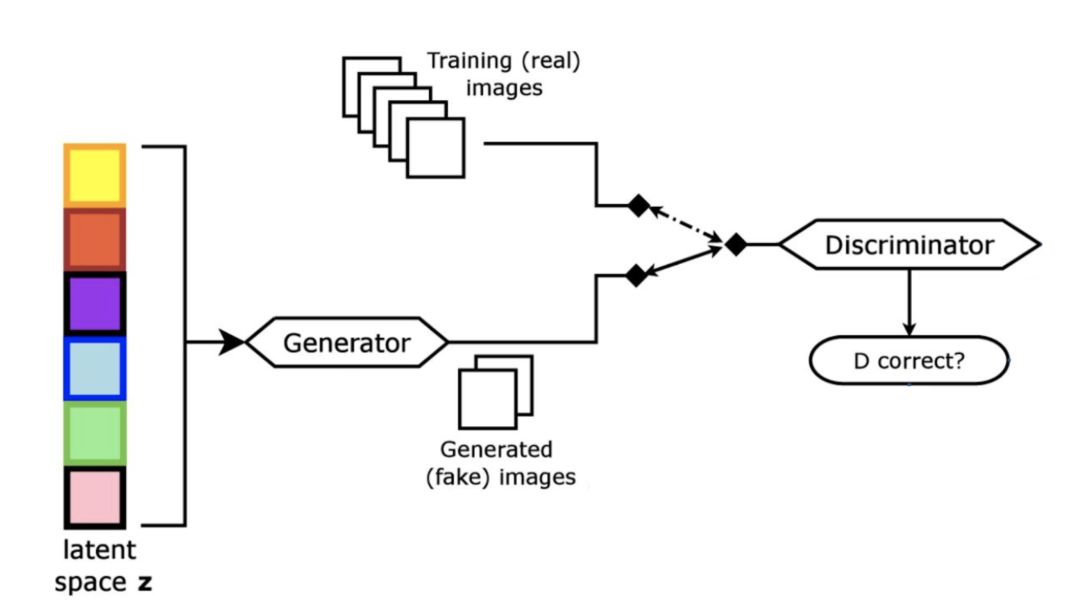
要回答这个问题，我们需要首先了解GANs的基础知识。
GAN是两个神经网络的组合，即:
